• Accueil
• Résumé
• Étude
• Vidéos de simulations
• Cadre de l'étude
• Contact

Hypothèses du modèle

Pour réaliser le modèle, nous avons dû poser quelques hypothèses :

1. Concernant la horde
   • Déplacement d’un seul manchot à chaque étape
   • Horde non scindée et sans trou
   • Chaque manchot a au moins 2 voisins
2. Concernant le vent
• Irrotationnel
• Constant au loin de la horde
• Indépendant de l’altitude
3. Concernant la température
• Uniforme et constante au sein de la horde
• Uniforme et constante au loin de la horde
• Pas de source de chaleur à l'extérieur de la horde

Modèle utilisé

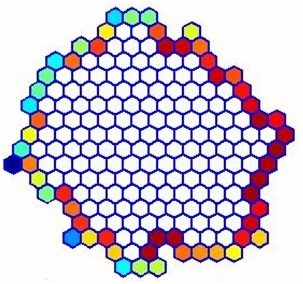
On génère aléatoirement une horde initiale, où chaque manchot est représenté par un hexagone.
Par cette représentation, on tient compte de la compacité de la horde.

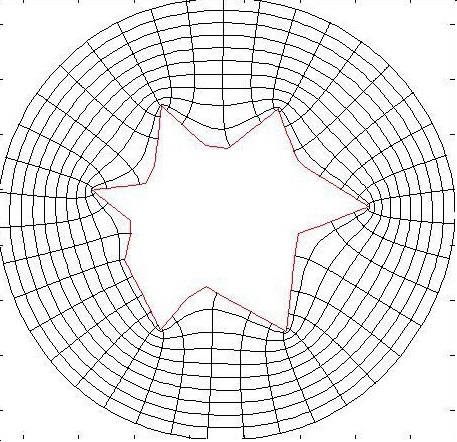
Sur la figure sont représentés deux polygones qui correspondent à deux modèles différents. Le domaine d'étude sera l'extérieur du polygone étudié.

Problème

On doit déterminer le vent et la température sur un domaine du type suivant:

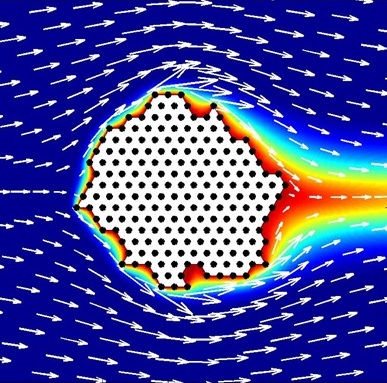
On obtient ce type de résultat pour une étape donnée:



Les flèches indiquent la direction du vent, la couleur la temperature (rouge=chaud, bleu=froid).
On remarque bien que le vent est dévié par l'obstacle compact formé par le groupe d'oiseaux.

Méthodes

1. Résolution pour une étape
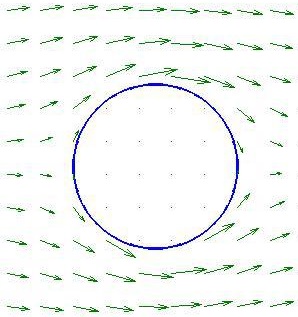
   • On détermine la température et le vent autour du disque unité. On doit notamment résoudre des équations aux dérivées partielles par une méthode de différences finies.
   • On transpose les solutions sur notre domaine d'étude par applications conformes (Joukovski et Schwarz-Christoffel).


2. Modification du domaine d'étude
• Détermination du manchot qui a le plus froid
• Détermination de la position la plus chaude sur la frontière
• Déplacer le manchot qui a le plus froid vers la position la plus chaude


3. Retour à l'étape 1.

Résultats

Voir les vidéos de simulations !