Modélisation de l'évolution d'une horde de manchots
dans des conditions climatiques extrêmes
                                                     

Introduction
Version détaillée :


Objectifs de l'étude

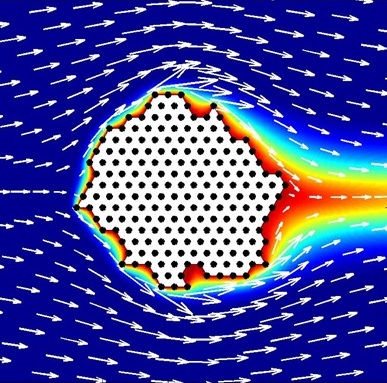
      Comme nous le présentions sur la page d'accueil, le phénomène de la tortue permet aux manchots de se réchauffer lors de conditions climatiques extrêmes. L'idée est ici de modéliser et simuler ce phénomène afin de pouvoir prédire l'évolution d'une horde de manchot sur la banquise en fonction de différents paramètres comme par exemple la vitesse du vent. Pour cela, il nous faut déterminer les déplacements individuels des manchots. Dans notre étude, on considère que le manchot qui se déplace est celui qui a le plus froid et qu'il ira se positionner à la position la plus chaude qui lui est accessible. On dira qu'un manchot a froid si il a une perte de chaleur élevée, et qu'il a chaud si cette perte de chaleur est basse. Voir la méthode.
      Alors, le problème consiste à déterminer la température en tout point situé aux alentours de la horde afin de déterminer les déplacements à effectuer. Cela nécessite également la connaissance du vent car la température en dépend directement. Un de nos objectifs est également d'évaluer la stratégie adoptée par les manchots en terme d'efficacité. Différents relevés doivent alors être effectués durant les simulations.


Hypothèses du modèle

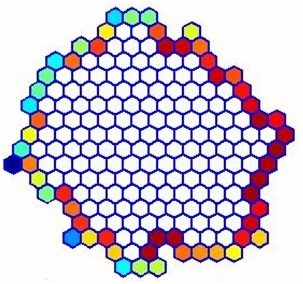
      L' hypothèse principale sur laquelle reposera l'étude est la suivante : Au sein de la horde, chaque individu souhaite augmenter sa propre température corporelle. Les manchots ne cherchent donc pas à augmenter la température globale de la horde. Ils raisonnent en tant qu'individus et non en tant que membres d'un groupe. Comme dans tout modèle, nous avons dû poser quelques hypothèses que nous présentons ci-dessous :
  • Concernant la horde de manchots
    •      La horde d'oiseaux forme un ensemble compact de sorte à ne pas y laisser entrer le vent. De plus, chaque manchot est en contact avec au moins deux autres manchots afin de se tenir au chaud. Nous supposons qu'un seul manchot se déplace à la fois et que de par la compacité de la horde, il ne peut se positionner que sur le pourtour de celle-ci. La horde ne forme toujours qu'une seule partie. Elle ne peut se scinder.
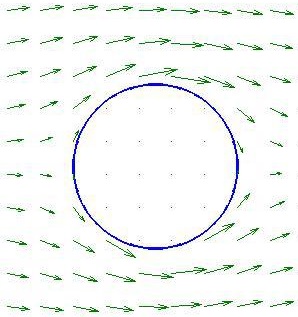
  • Concernant le vent et la température
    •       Du fait de la petite taille des manchots (<120cm), nous négligeons les phénomènes liés à l'altitude pour le vent et la température. Ainsi, notre domaine de résolution sera un domaine du plan.
         Dans cette étude, nous nous intéressons au cas où le vent est constant au large de la horde. De plus, nous supposons qu'il n'est pas tourbillonnant, même en présence de l'obstacle que représente la horde.
          La température au sein de la horde est supposée être la même en tout point et ne varie pas au cours du temps de simulation. Nous verrons alors dans la suite de quelle manière nous quantifions la sensation de froid qu'a un manchot. La température dans les zones éloignées de la horde connaît une répartition uniforme et sa valeur ne change pas au cours du temps.
          Toujours concernant la température, nous considérons qu'il n'y a aucune source de chaleur en présence sur le domaine d'étude (l'extérieur de la horde). Nous négligeons ainsi par exemple la chaleur que pourraient renvoyer les manchots à l'extérieur de la horde.


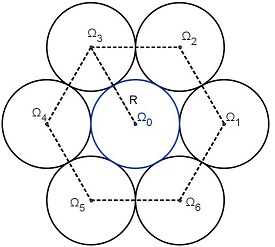
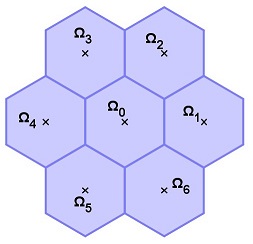
Structure de la horde

      Pour commencer, il nous a fallu faire le choix de la forme géométrique utilisée pour modéliser un manchot. Pour cela, nous sommes partis d'un constat simple qui est qu'un manchot vu de dessus peut être représenté par un disque étant donnée sa forme régulière et cylindrique. La horde pourrait donc être modélisée par un ensemble de disques adjacents, comme illustré sur la première des figures ci-dessous. Seulement, afin de rendre compte de la compacité de la horde, nous avons décidé de remplacer les disques par les hexagones présents sur la deuxième figure. En effet, les manchots sont tellement serrés les uns contre les autres que leur corps épouse la forme des manchots voisins.
                                


Domaine de résolution

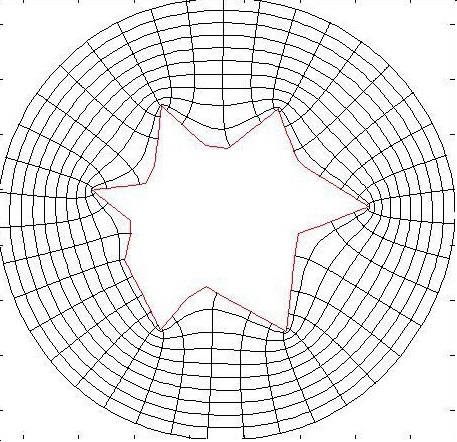
     Considérons la horde de manchots représentée ci-dessous. Comme nous le verrons dans la suite de l'étude, nous avons choisi de tester deux modèles utilisant des domaines de résolution différents. Pour le premier modèle, nous choisissons le polygone P1 passant par les centres des manchots situés en bordure de horde. Pour le second modèle, nous considérons le polygone P2 qui décrit le contour de la horde.

     Nous définissons alors le domaine de résolution Ω qui dans les deux modèles correspond à l'extérieur du polygone (P1 ou P2). Ce domaine est alors un sous ensemble connexe et non borné du plan. On constate alors que le problème possède deux particularités qu'il faudra savoir gérer :
  • Le domaine de résolution a une forme assez complexe et plutôt irrégulière
  • Le domaine de résolution change à chaque fois qu'un manchot modifie sa position.



Suite de l'étude