Modélisation de l'évolution d'une horde de manchots
dans des conditions climatiques extrêmes
dans des conditions climatiques extrêmes
Résolution numérique
Version détaillée :
Après avoir démontré dans les parties précédentes les méthodes utilisées, il est temps de passer à la résolution numérique du problème de détermination de la température et du vent sur le domaine extérieur de la horde de manchots. Afin d'illustrer les méthodes utilisées, nous proposons le diagramme suivant :
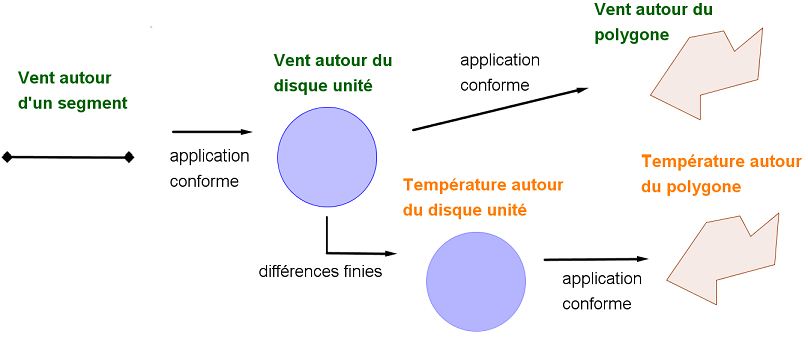
L'étape qui nous intéresse ici est celle de la détermination de la température autour du disque unité en connaissant déjà le vent sur ce domaine. Pour cela, il nous faut résoudre l'équation de convection-diffusion obtenue précédemment :
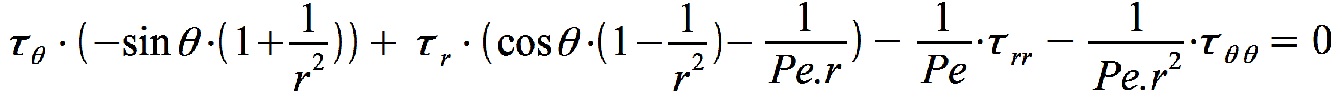
Cette équation aux dérivées partielles (EDP) ne pouvant être résolue analytiquement, nous avons utilisé une méthode des différences finies. Ce type de méthode consiste à discrétiser notre domaine de résolution à l'aide d'un maillage afin d'obtenir un nombre fini (mais grand) de points auxquels nous calculons une solution approchée de la température. Pour cela, en chacun des points du maillage, nous réécrivons l'équation précédente en remplaçant chaque dérivée partielle par un taux d'accroissement bien choisi qui met en jeu les noeuds voisins. Ainsi, on obtient un certain nombre d'equations linéaires reliant les différentes solutions en chacun des noeuds.
En fait, approcher la solution d'une EDP revient à résoudre un système d'équations linéaires. Sa taille (égale au nombre d'inconnues) dépend directement du nombre de noeuds du maillage. On réalise alors qu'il faut toujours trouver un compromis dans ce type de problème. Pour augmenter la précision de la méthode, il faut augmenter le nombre de noeuds du maillage. Mais cela fait grandir la taille du système à résoudre et donc le temps de calcul par l'ordinateur. Les façons de gérer ces compromis et d'optimiser la methode sont enseignées dans les cours d'analyse numérique.
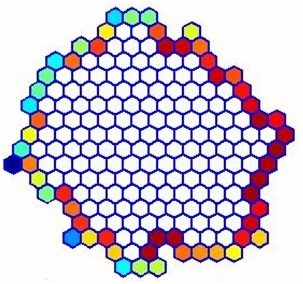
Étant donnée la forme annulaire du domaine de résolution, nous choisissons naturellement un maillage polaire. Sur la figure ci-dessous, vous pouvez voir la forme du maillage utilisé pour la résolution ainsi que son image une fois transformé par application conforme autour d'un polygone.
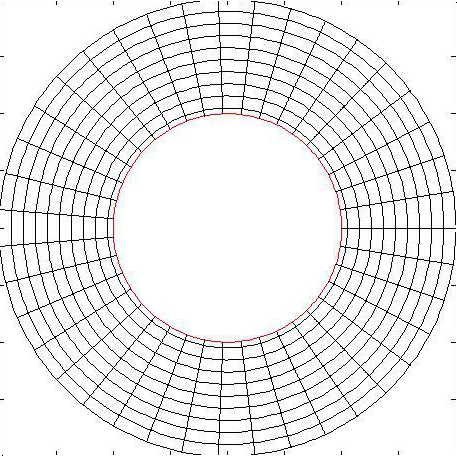
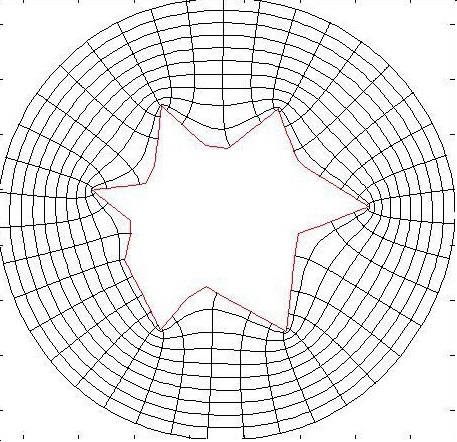
Le maillage utilisé en pratique est en fait bien plus précis que celui-ci. Les noeuds sont plus rapprochés et plus nombreux. En réalité, pour les simulations , nous travaillons avec 45 000 noeuds. Ce qui signifie résoudre 45 000 équations à 45 000 inconnues. Pour information, un ordinateur moyen met environ 15 secondes pour résoudre ce problème.
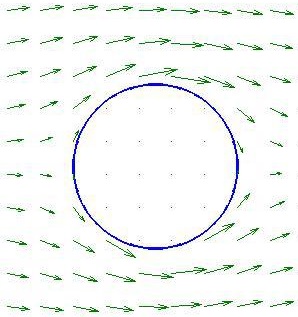
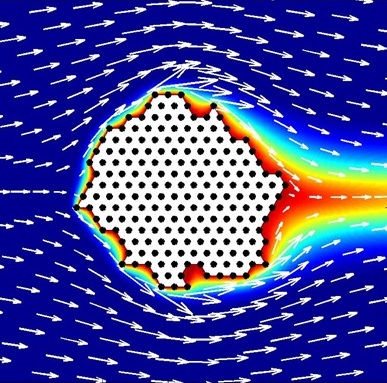
Et voici le résultat obtenu avec cette précision pour un vent venant de la gauche :

Chapitre précédent
Suite de l'étude