Modélisation de l'évolution d'une horde de manchots
dans des conditions climatiques extrêmes
dans des conditions climatiques extrêmes
Vent
Version détaillée :
Dans l'intégralité de l'étude, nous considérons un vent venant de la gauche. Comme nous l'avons vu sur le diagramme de la section précédente, il nous "suffit" de déterminer le vent autour d'un segment pour ensuite l'obtenir autour de notre polygone en composant avec des applications conformes. Mais encore faut-il démontrer que l'on puisse faire passer une solution d'un domaine à un autre. Et avant cela, il faut caractériser la solution en déterminant les équations qui régissent le vent.
Équations du vent
C'est dans cette partie que l'on utilise l'hypothèse principale posée sur le vent disant qu'il est irrotationnel. Grâce à celle-ci et en utilisant la décomposition de Helmholtz-Hodge, on arrive à démontrer que le vent s'écrit comme le gradient d'un potentiel. On notera alors :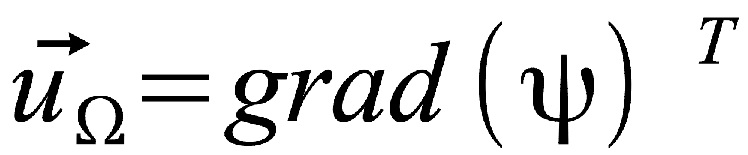
Dans la suite de l'étude on cherchera alors à déterminer le potentiel pour ensuite en déduire le vent par dérivation.
En sachant que le vent est un phénomène sans source, on utilise le théorème de Gauss qui implique que :
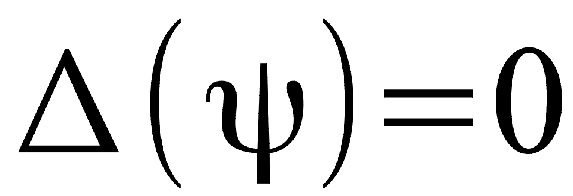
Il faut maintenant ajouter à cela une condition au bord de la horde. En effet, le vent n'entre pas dans la horde et cela se traduit par un flux nul au travers de la frontière.
C'est ainsi que l'on obtient le système d'équations suivant pour le vent :
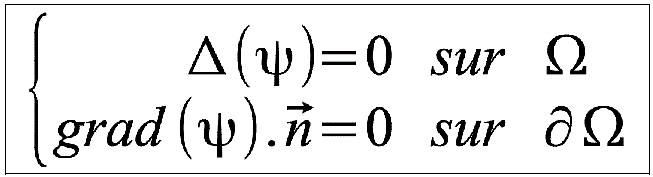
Passage de la solution d'un domaine à un autre
Maintenant que l'on a caractérisé la solution pour le vent, on souhaite la faire passer d'un domaine à un autre comme par exemple de l'extérieur d'un segment à l'extérieur d'un disque. Dans la section précédente, on a montré l'existence d'une application mettant en bijection ces deux domaines. Il faut maintenant démontrer qu'en composant une solution sur le premier domaine avec l'application en question, on obtient une solution sur le second domaine.Pour cela, on doit montrer que la composée vérifie les équations du vent également. Ce qui nous sauve dans cette partie est le fait que l'application est conforme et donc qu'on peut utiliser les équations de Cauchy-Riemann. Les calculs sont détaillés dans le pdf qui concerne cette partie.
Vent autour d'un segment
Il reste maintenant à déterminer le vent sur un domaine simple. Le segment fait un candidat idéal car son épaisseur étant nulle, il n'oppose aucune résistance s'il est placé dans le sens du vent.Voici une représentation de la situation :

On remarque qu'en tout point du segment, la normale est bien orthogonale au vent. La deuxième équation du vent est bien vérifiée.
On obtient dans cette configuration les expressions suivantes pour le vent et pour son potentiel :
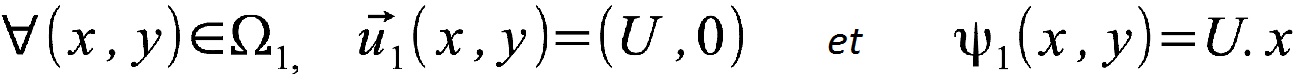
Ce potentiel est bien de Laplacien nul. Les deux équations du vent sont bien vérifiées.
Vent autour d'un disque
Nous obtenons la solution autour du disque unité en utilisant l'application de Joukovski. L'expression de cette application étant assez simple, on peut déterminer de manière explicite la solution autour du disque. On obtient :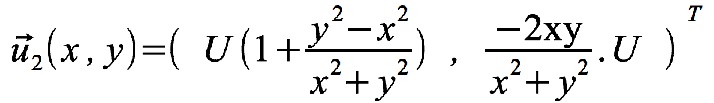
Voici l'illustration du résultat :
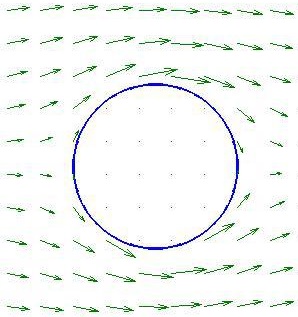
Vent autour d'un polygone
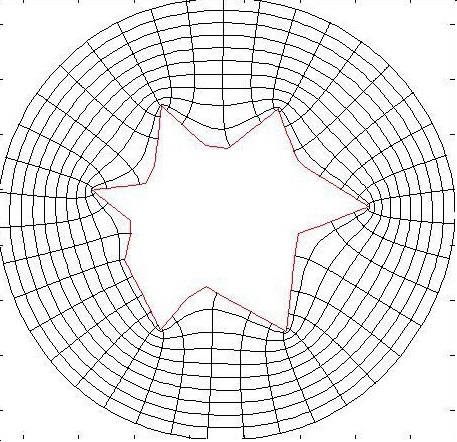
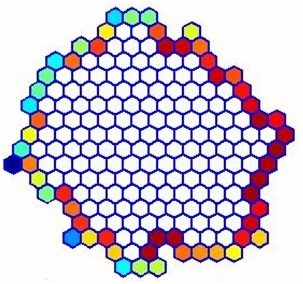
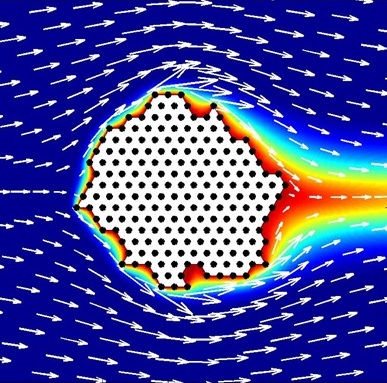
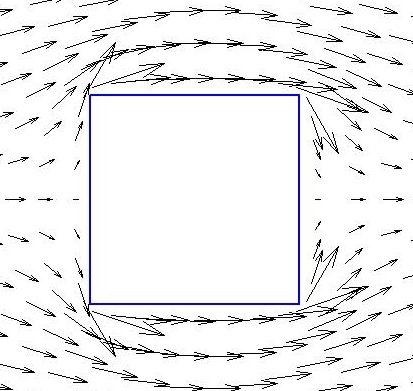
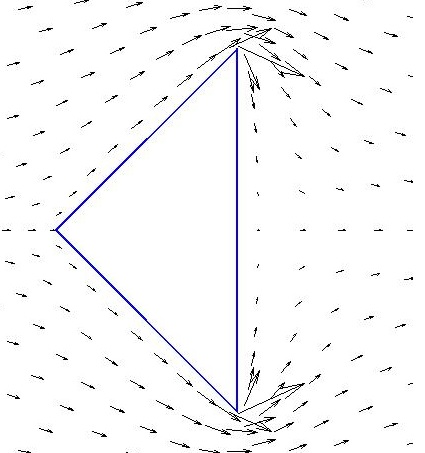
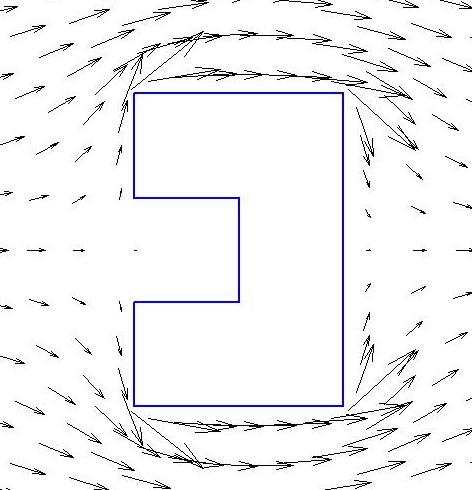
Il ne nous reste plus qu'à utiliser l'application de Schwarz-Christoffel pour obtenir la solution autour du polygone de notre choix. Cette application étant beaucoup plus complexe que celle de Joukovski, on ne détermine pas explicitement la solution. On utilise alors le package Matlab créé par Tobin A. Driscoll.Voici les résultats obtenus pour différents polygones :

Chapitre précédent
Suite de l'étude