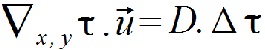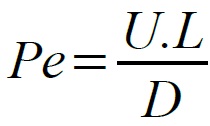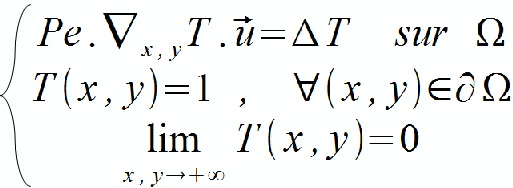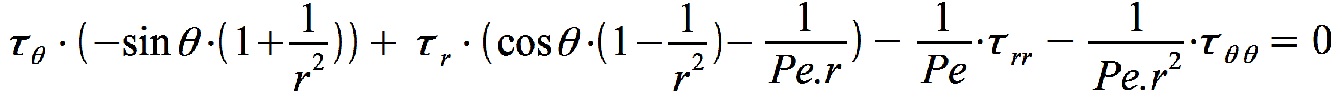Modélisation de l'évolution d'une horde de manchots
dans des conditions climatiques extrêmes
Température
Version détaillée :

Équation de la température
Notons tout d'abord l'équation de convection diffusion qui fait le lien entre le vent et la température :
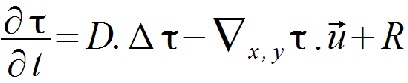
Avec :
- 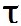 la température
-
la température
- 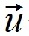 le vent
le vent
- t le temps
- R est une source de chaleur
- D le coefficient de diffusivité thermique
- x et y les variables spatiales
Or nous avons supposé qu'il n'y avait pas de source de chaleur. De plus, on résout le problème étape par étape, et à une étape donnée, le système est à l'équilibre. Il
ne dépend alors pas du temps. Notre équation de convection diffusion devient ainsi :
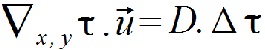
On normalise ensuite l'équation de sorte que la température au sein de la horde soit égale à 1, et à 0 au loin de la horde.
On introduit par la même occasion le nombre de Péclet (noté Pe) de la façon suivante :
Avec L le diamètre de la horde dans le cas où elle aurait une forme circulaire, et U la vitesse constante du vent, on a :
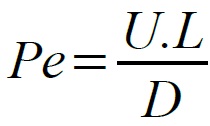
On a alors après normalisation de l'équation les conditions et le problème suivants :
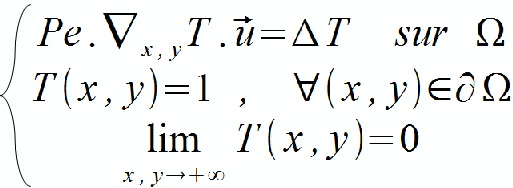
Passage d'un domaine à un autre
On va maintenant déterminer la température autour du disque unité parce qu'autour de celui-ci, on connait déjà le vent grâce à l'application de Joukowski, et aussi parce qu'un maillage se met facilement
en place autour du disque.
On aura alors un domaine de résolution du type suivant, compris entre l'extérieur du disque unité et un bord artificiel créé par nous même dont on pourra décider le rayon.

Note : Nous avons vérifié que l'on pouvait passer d'un domaine à un autre de façon similaire à celle employée avec le vent.
Température autour du disque
Sur ce domaine, les coordonnées polaires s'imposent. Suite à un changement de variables, notre équation de convection diffusion s'écrit alors :
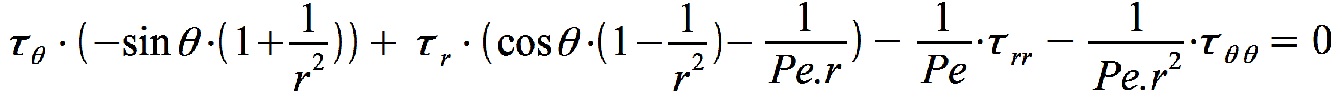
Avec les conditions aux limites suivantes :
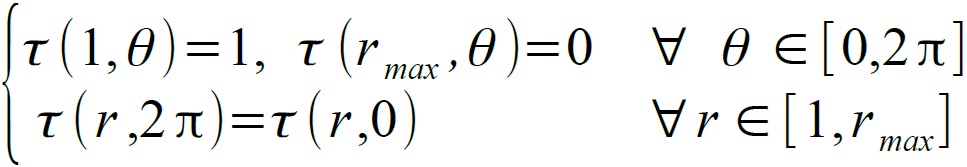
Chapitre précédent
Suite de l'étude
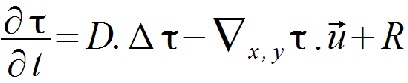
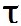 la température
-
la température
- 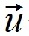 le vent
le vent