Modélisation de l'évolution d'une horde de manchots
dans des conditions climatiques extrêmes
dans des conditions climatiques extrêmes
Applications conformes
Version détaillée :
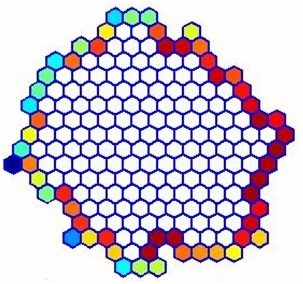
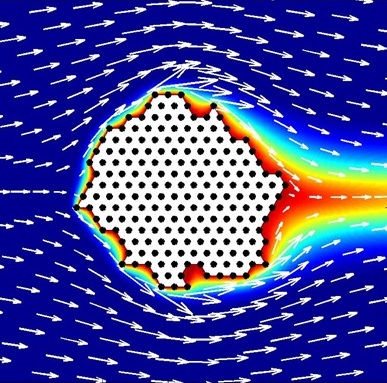
Lorsque la horde est constituée et après chaque déplacement d'un manchot, il faut déterminer le vent et la température sur un domaine de la forme suivante :

Comme nous le verrons dans les parties suivantes, le vent et la température sont régis par des équations aux dérivées partielles, que l'on ne peut pas résoudre directement sur un domaine trop complexe comme celui-ci. L'idée est alors de résoudre le problème sur des domaines beaucoup plus réguliers pour ensuite transposer les solutions sur notre domaine d'étude. Et c'est ici qu'interviennent les applications conformes.
Une application conforme est une fonction complexe qui possède certaines propriétés comme la conservation des angles ou le fait qu'elle soit holomorphe (dérivable) ce qui nous permettra d'utiliser les équations de Cauchy-Riemann (relations entre les différentes dérivées partielles). L'enjeu est alors de trouver une application conforme qui met en bijection les deux domaines en question (celui où l'on connait la solution et notre vrai domaine d'étude) mais surtout de démontrer que l'on peut passer les solutions d'un domaine à un autre grâce à cette même application. Et c'est là qu'interviennent les équations de Cauchy-Riemann !
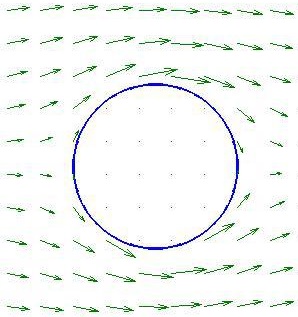
Comme nous le verrons dans les deux sections suivantes, le vent se détermine très facilement sur le domaine correspondant à l'exterieur d'un segment alors que la température sera obtenue sur l'extérieur du disque unité. Et cela tombe très bien car nous disposons de deux applications conformes qui permettent de faire les transpositions nécessaires :
- La transformation de Joukovski qui envoie l'extérieur du disque unité sur l'extérieur du segment d'extrémités (-2,0) et (2,0). Notons que cette application est souvent utilisée en aéronautique car elle permet également de mettre en bijection un cercle avec un profil d'aile d'avion. Il est alors aisé d'étudier l'écoulement d'air autour d'une aile.
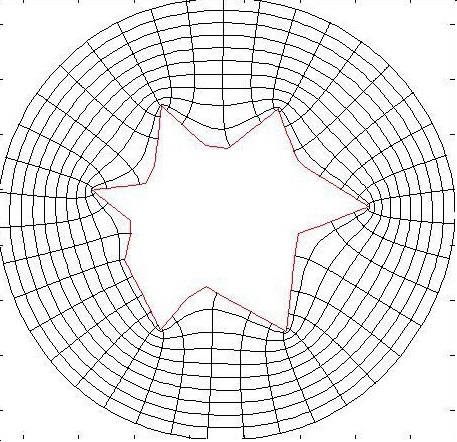
- L' application de Schwarz-Christoffel qui envoie le disque unité sur l'extérieur du polygone de notre choix. L'application étant paramétrée par la donnée des sommets du polygone. Dans notre cas, nous devons considérer l'extérieur du disque unité. Il faudra alors également composer avec une inversion z -> 1/z.
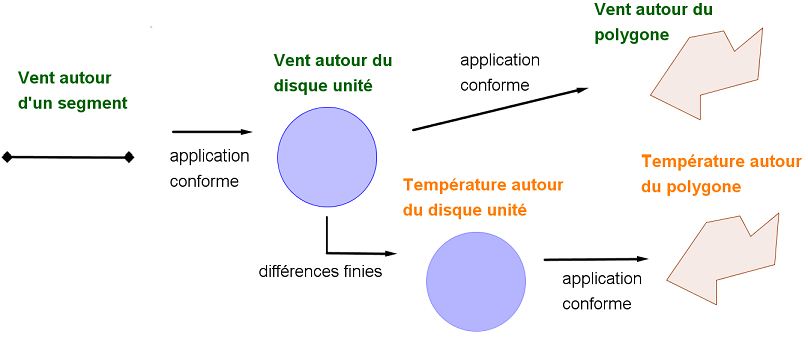
Voici alors le schéma global de l'étude :
Chapitre précédent
Suite de l'étude